Port-based approach of complex distributed-parameter system models for analysis and simulation (PACDAS, STW-TWI.6012)

The Problem of the Initial Guess for an Iterative FEM Solution

In the case of a large sparse matrix, the linear equations are usually solved with an iterative method (see for example http://www.netlib.org/templates). The initial guess can speed up the convergence enormously. I have looked at electrostatic problems in 2D, and tested several initial guesses. I came up with a scheme which works well in many cases.

A FEM with two potential surfaces is generally governed by two functions if no specific information is given: the total areas (A1(R1) and A2(R2)) of the space at a given (minimal) distance (R1 and R2) to each of the surfaces with a constant potential (V1 and V2). The initial guess for potential a given point at distances R1 and R2 of potential surfaces V1 and V2:

where S1 and S2 are respectively the squareroots of the relative area with respect to the potential surface areas.

The idea is that the problem is mapped to a simple dipole problem, the "dimension" follows from the ratio of area:distance. The dipole charges have spatial extension. However, this led to a under-estimation of the potential. The finite-volume effects (a relatively small grid, with periodic boundary conditions) yield the squareroot, rather than the standard logarithm, "fundamental solution" as more appropriate.

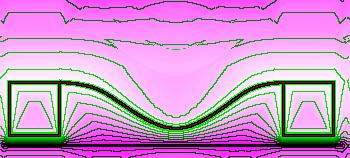
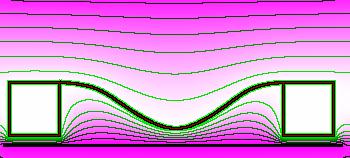
(The problem of the electroelastic beam, on a 350x158 grid. Initial guess left, final solution right.)

(A model problem with large variations in electric field strength, on a 284x221 grid. Initial guess left, final solution right.)

A C-code snippet picks a picture, interpret white as background, red as V1=1.0, and black as V2=0.0, and produces these solutions. Periodic boundary conditions are used. The iterative method is a diffusion type method.