Port-based approach of complex distributed-parameter system models for analysis and simulation (PACDAS, STW-TWI.6012)

The deformation of a table, depending on the fixture position

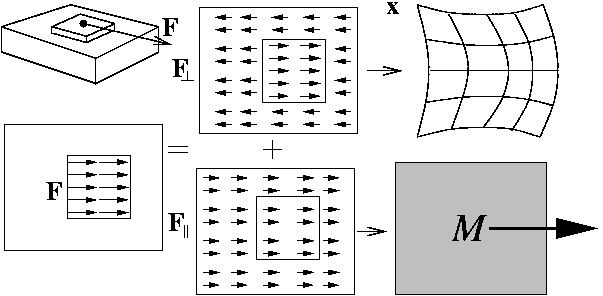
For a table we can decompose the situation of a constant force into a constant acceleration rigid-body part, and a static (time-independent) deformation. The latter is an excellent starting point for the modes of a reduced model of the displacement.

In a 20x20 FEM model of the longitudinal deformation of a table, we can see the different modes depending on the deformation.

The typical filling of the stiffness matrix; red are positive entries, blue are negative entries.

In the case of the central fixture, only one of the four dominant modes is excited by the applied force. All the "odd modes" are absent. The black dots are the reference positions, the red dots the displaced positions.

In the case of the front fixture, many more modes are excited. (The displacement is scaled down with respect to the central-fixture picture by a factor of two.)

The model, with the central fixture, was used to compare different model-reduction approaches. The model reduction with the modes of the static-deformation expansion are compared with the vibrational modes. The pulse-shaped force was applied to the fixture, and deviation of the corner of the table from the rigid-body motion was tracked. The second-order static-deformation model is hardly distinguishable from the full results, indicating the superiority of this approach.