Point and Line Interpolated Surfaces (PaLIS)

smooth organic forms usually require a lot of effort to generate in computer graphics. Either a large number of points are used for a simplex construction, which is smoothen (blurred) afterwards. Or complicated geometrical definitions, with control points and vectors are used to generate surfaces.
Another problem is to match the edges smoothly, and allow for variations in the number of control points. (NURBS is one of the more efficient algorithms.)
I developed a method, which I call PaLIS (Point and Line Interpolated Surfaces), which require only a number of points on the surface and a value for the RIGIDITY at these points.
The examples here are "blobs" defined by two and six points, with varying rigidity.

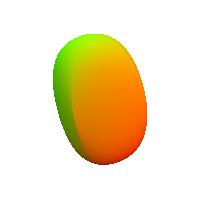
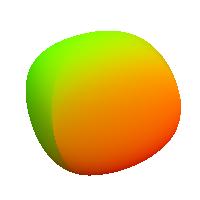
the two-point blobs with rigidity 1, 3, and 5.

The points are at (0,0,1) and (0,0,-1), and the objects consist of four surfaces.

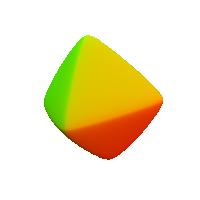
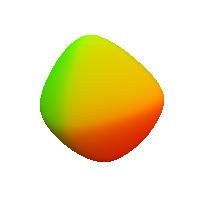
the six-point blobs with rigidity 0.5, 1, 3, and 5.

The points are at (1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) and (0,0,-1), and the objects consist of eight surfaces.
Note that only one parameter connect each row of shapes, also note that between small and large rigidity the shape varies between the dual forms: the tetraeder and the cube, since in one limit the corner is the center of the face in the other limit.
The lighting is determined with the analytical form for the surface normal. These examples are test cases, as the method is designed for surfaces with four corners, the two- and three-corner surfaces here are defined implicitly. No smoothing or interlacing is applied (except the jpg DCT, for file compression).

The surfaces have intrinsic coordinates. As an example a six-point surface with rigidity 2, and a two-point surface with rigidity 4, with a mesh mapped on it.

No special functions were used, only polynomials of degree 4 and less are required.
Details later (from January 2006 I started writing up the details for a scientific publication).