Port-based approach of complex distributed-parameter system models for analysis and simulation (PACDAS, STW-TWI.6012)

Dynamics of nonlinear Hamiltonians

A Hamiltonian of an elastic beam is given as a polynomial with about 220 terms, to fourth order. The system can be used to find a minimal, or static, solution, using dissipation, which is the Control-Engineering version of a Conjugate Gradient approach.

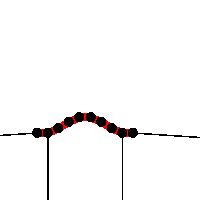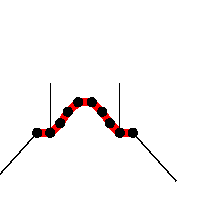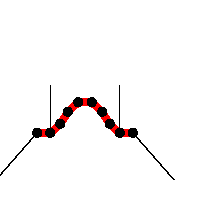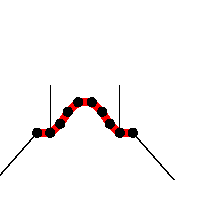
The black lines represent the resultant forces on the boundary nodes. Eventually, the sum force is zero.

The same hamiltonian and the same state can be used for a dynamical simulation, which conserves energy, not explicitly, but to 5 decimal places for 3000 time steps. One end of the beam is suddenly released from the clamped boundary conditions. The bending dynamics is generally much slower than the longitudinal vibration dynamics.

The code is written in C, and uses the libraries of libplot and lapack. It consists of two separate codes: 1) the generation of the Hamiltonian, written as a data file, 2) the simulation of the Hamiltonian, with stepsize and damping, and multiple data output. The evaluation (functional derivative) costs about three times the total number of factors in the Hamiltonian in floating-point operations. The improved integration step using the last and previous gradients. The simulation tests for stepsize errors, by calculating the energy in the system. The simulations above take only seconds to run, where I/O account for most of the computing time.

The frequency spectrum can be calculated around every state, however, it makes only sense to calculate the spectrum around a static solution. Otherwise, negative eigenvalues might appear associated with the overall motion of the system. Most codes, especially linear, and linearized, will have major problems reproducing strain effects in vibrational analysis. Starting from physical principles, such results come, more or less, for free.

More about these results, including an analysis of the changing frequencies of the strained systems, for various boundary conditions, can be found in the slides of the talk at the 25th Benelux meeting The minimal model of a continuous, physical system, and more. Some interesting singularities (bifurcations?) in the vibrational modes appear for large deformations. For the supported beam this is easily understood: if the two endpoints are brought together, the beam can rotated freely around the common endpoint, which corresponds to a zero eigenfrequency. That similar effects occur for all the other boundary conditions was not expected.

Comment added on 17-8-2006:

Further study revealed these bifurcations are typical of large deformations. Euler already investigated this first. Most studies focus around the existence of stable solutions; local minima in the elastic energy. In our case we discovered the "singular behavior" of jumping from one minimum to the next. The behavior, in our case, is not singular, as the kinetic energy is taken into account. A short overview is given on slide 7 of the presentation of: the sixth PACDAS project meeting at Oce in Venlo